Parallel computing is of paramount importance for the scientific community as it allows to carry the execution of calculations simultaneously, leading to a significant cut in computation time. In this post, I will show you how do I parallelize computation across the CPU threads using python. I will illustrate the latter through an example: the estimation of Pi using Monte Carlo simulation.

Design of the parallelization framework

Going straight to the point, we would like to parallelize a task across N CPU threads. The first step is to identify the data on which we would like to parallelize computation, so that the data elements are independent. Second, we need to define the task to be parallelized: a function that takes as input a list of data elements and performs the desired task using these data, and eventually return a result. Instances of this function will run separately in the N threads. Finally, if needed, we can define a function perform some post processing.

Example: estimating $\pi$ with Monte Carlo

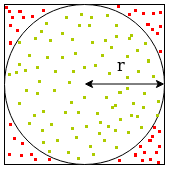
Let's take as an example the task of estimating $\pi$ through Monte Carlo method. Briefly, the method consists of randomly generating a large number of points within a square having a side length of $2r$. Then, we count the points that fall inside the circle having radius $r$ inscribed in the square. The approximation of $\pi$ is then $4$ times the probability that a generated point falls inside the circle, as shown below:

$$ P(\text{generated point falls inside the circle}) = \frac{\text{area of the circle}}{\text{area of the square}} = \frac{\pi r^2}{4 r^2} = \frac{\pi}{4} $$

On the other hand, if $m$ is the number of generated points and $m_c$ the number of points falling inside the circle, then by Monte Carlo we obtain:

$$ P(\text{generated point falls inside the circle}) \underset{\text{$m$ large}}{\approx} \frac{m_c}{m} $$

Hence, $$ \pi \underset{\text{$m$ large}}{\approx} 4 \times \frac{m_c}{m} $$

The more data points we generate, the more accurate is the approximation of $\pi$.

The parallelization code

There are many python packages that make the parallelization pipeline easy and simple. I introduce here the lightweight mpyll package that follows the design above.

First, we define the list of data on which we will parallelize the computation. The data here would be the randomly sampled points.

import numpy as np
from mpyll import parallelize

r = 1. # the radius
m = 10 ** 6 # the number of points to generate
X = np.random.uniform(-r, r, size = m) # the x-coordinates of the data points
Y = np.random.uniform(-r, r, size = m) # the y-coordinates of the data points
data = [(X[i], Y[i]) for i in range(m)] # define the list of points

Next, we define the task to be parallelized. The function takes as argument a list of points as well as other arguments, and returns the number of points falling inside the circle.

def count_in_circle_points(data, r, m):
    a = np.array(data) # matrix, each row contains a point coordinates
    d = np.sqrt(np.sum(a ** 2, axis = 1)) # distance to the origin
    in_circle = d <= r # an array, True if distance <= radius, False otherwise
    return np.sum(in_circle)

Since this task will be run in separate processes, mpyll provides a shared memory that is used to store the data returned by the parallelized task.

Finally, we define a post processing function that takes as argument the list of the parallelized task outputs contained in the shared memory and returns the final result.

def estimate_pi(data, m):
    pi_estimation = 4. * np.sum(data) / m
    return pi_estimation

In order to execute the parallel computation, we simply call the parallelize function. Note that one could pass additional arguments to the task and the post processing functions. The arguments' names should start with the name of the task or the post processor, followed by an underscore and the name of the argument. The number of threads to be used is passed in n_jobs argument. A value of -1 means use all available threads.

pi_estimation = parallelize(task = count_in_circle_points,
                            data = data,
                            post_processor = estimate_pi,
                            n_jobs = -1,
                            # task arguments
                            count_in_circle_points_r = r,
                            count_in_circle_points_m = m,
                            # post processor arguments
                            estimate_pi_m = m)