Anonymous walk embeddings: the growth of anonymous walks with length
May 03, 2020 at 04:30 PM,
by
Mehdi
graph embedding
data science
representation learning
node embedding
Graph embedding is a field of representation learning aiming to transform a graph into a vector of features (numbers) that captures the structural aspect of the graph and/or its node features. One of these techniques is the Anonymous Walk Embeddings designed by Sergey Ivanov and Evgeny Burnaev.
In their paper, the authors introduced the feature-based anonymous walk embedding model, in which, each feature $i$ in the embedding vector corresponds to the probability of observing the anonymous walk $a_i$, after anonymizing many generated random walks of length $l$ starting from different nodes in the graph. The size of the embedding is in function of the length of the generated random walks. This growth is shown in the Figure 2 of the paper.
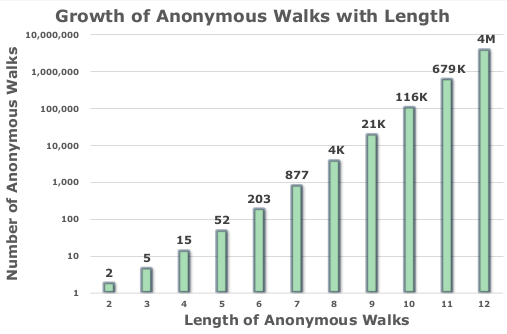
As shown in the figure, the authors did not provide the actual numbers starting from $l = 8$. These are the numbers for those who may be interested (e.g. implementation testing).
| Length of walk | Number of anonymous walks |
|---|---|
| 8 | 4140 |
| 9 | 21147 |
| 10 | 115975 |
| 11 | 678570 |
| 12 | 4213597 |
| 13 | 27644437 |
Clearly, the feature-based AWE becomes unusable when $l \ge 8$ because the sparsity of the embeddings becomes more pronounced with the growth of the length of the random walks.
When computing the embeddings of many graphs using the same length, the consistency of the embeddings should be preserved. I mean by "consistency" the fact that for two given graphs, the $i^{\text{th}}$ feature should correspond the $i^{\text{th}}$ anonymous walk. For that, we need to enumerate all possible anonymous walks given a certain length. The python implementation below does the job.
The idea of the algorithm is that we can imagine the anonymous walks as a tree of depth $l$ (length of the walks), in which each node holds two values: (i) the anonymous identifier (1, 2, ...) and (ii) the maximum identifier of its predecessors' lineage.
class AWNode(object):
def __init__(self, data, maxi):
self.data = data
self.maxi = maxi
self.parent = None
self.children = list()
def add_child(self, child):
self.children.append(child)
child.parent = self
def add_children(self, children):
for child in children:
self.add_child(child)
class AWTree(object):
def __init__(self):
self.root = AWNode(data = 1, maxi = 1)
Next, we start from the root of the tree (id = 1, maxi = 1), then we develop the tree in a Breadth-First Search fashion until reaching the desired depth: to each node having an anonymous identifier $i$, we associate children having identifiers $\{1, 2, ..., i + 1\}$ and we set maxi to the maximum identifier of its predecessors.
def get_anonymous_walks(walk_length):
if not isinstance(walk_length, int) or walk_length < 1:
raise ValueError('Invalid walk length')
# develop tree
tree = AWTree()
leafs = [tree.root]
tree_level = 1
while tree_level < walk_length:
leafs_new = list()
for leaf in leafs:
children = [
AWNode(data = i, maxi = i if i > leaf.maxi else leaf.maxi)
for i in range(1, leaf.maxi + 2)
]
leaf.add_children(children)
leafs_new += children
leafs = leafs_new
tree_level += 1
# get walks
walks = list()
for leaf in leafs:
walk = list()
n = leaf
while n.parent != None:
walk.insert(0, n.data)
n = n.parent
walk.insert(0, 1)
walks.append(tuple(walk))
return walks
The final step consists of backtracking starting from each leaf and collecting anonymous identifiers until reaching the root.
This tarball contains all possible anonymous walks in function of the length of the generated random walks (doubly compressed to save some hosting storage).